Twitter proof: the Tower of Hanoi


< change language

In this post we prove what the minimum number of moves to solve the problem of the Tower of Hanoi is!

Claim: let $T(n)$ denote the number of moves it takes to solve the Tower of Hanoi with $n$ disks; then $T(n) = 2^{n}-1$.

Twitter proof: note that to solve the problem with $n$ disks, we first have to move the top $n-1$ disks to one of the two poles, move the bottom disk (the bigger one) to the remaining pole, and then move the top $n-1$ disks to the top of the bigger disk. Each time we move the top $n-1$ disks to another pole we must take, at least, $T(n-1)$ moves (by definition of $T$) hence we clearly have $T(n) = 2T(n-1) + 1$. Just notice that $B(n) = 2^n - 1$ satisfies the recurrence relation and that $T(0) = B(0) = 0$.

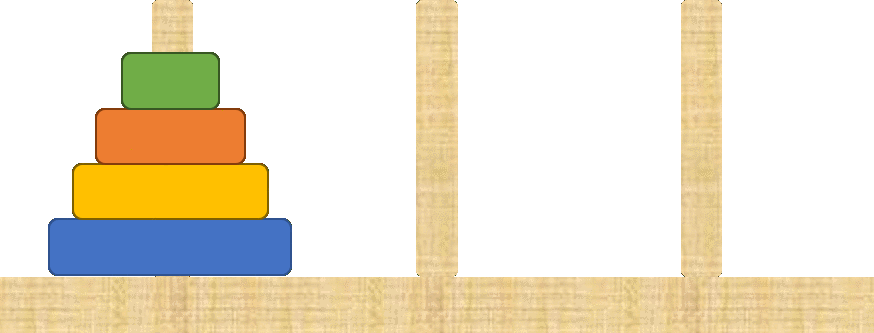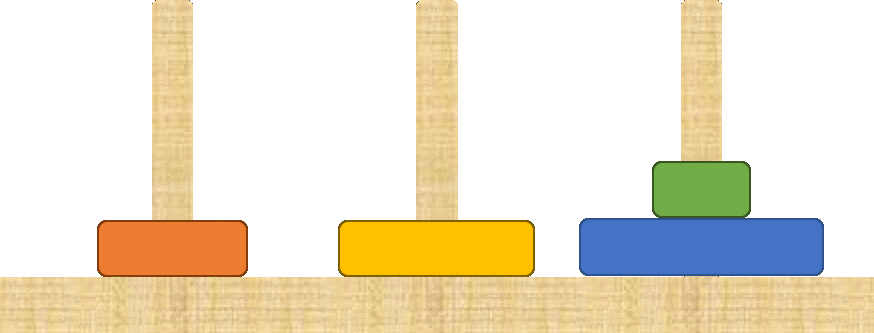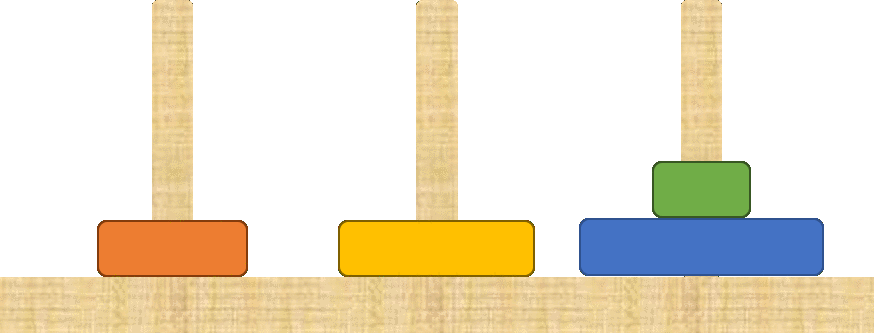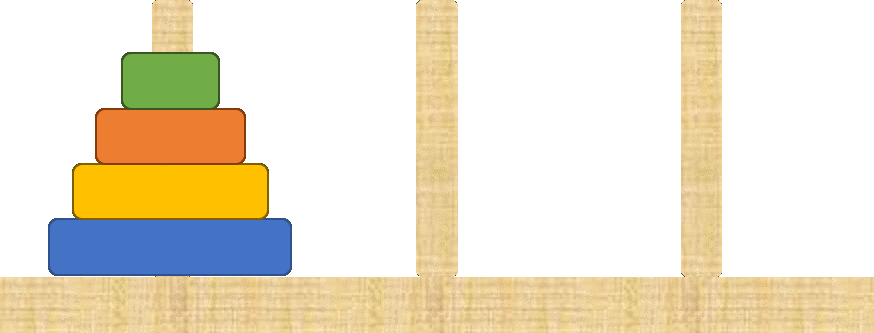
If you are having trouble understanding what I mean by to solve the problem with $n$ disks, we first have to move the top $n-1$ disks to one of the two poles, move the bottom disk (the bigger one) to the remaining pole, and then move the top $n-1$ disks to the top of the bigger disk, check the following sequence of images that contains some of the intermediate steps to solve the Tower of Hanoi with $4$ disks:


First we move the top $3$ disks to the centre pole in $T(3)$ moves...


Then we change the bottom disk to the available pole in $1$ move...


Then we move the top $3$ disks again in $T(3)$ moves!
Neste post vou provar qual é o número mínimo de movimentos necessário para resolver o problema da Torre de Hanoi!

Proposição: se $T(n)$ é o número mínimo de movimentos necessários para resolver o problema da Torre de Hanoi com $n$ discos, então $T(n) = 2^{n}-1$.

Prova num tweet: repare-se que para resolver o problema com $n$ discos, primeiro temos de mexer os $n-1$ discos mais pequenos para uma das duas varas livres, depois mexemos o maior disco para a outra vara vazia, depois voltamos a mexer os $n-1$ discos mais pequenos para cima do disco maior. De cada vez que mudamos os $n-1$ discos mais pequenos de vara, temos de fazer pelo menos $T(n-1)$ movimentos (pela definição de $T$) portanto temos claramente $T(n) = 2T(n-1) + 1$. Agora basta reparar que $B(n) = 2^n - 1$ satisfaz a relação de recurrência e que $T(0) = B(0) = 0$.

Se está a custar a entender o que quero dizer com para resolver o problema com $n$ discos, primeiro temos de mexer os $n-1$ discos mais pequenos para uma das duas varas livres, depois mexemos o maior disco para a outra vara vazia, depois voltamos a mexer os $n-1$ discos mais pequenos para cima do disco maior, vejam a sequência de imagens seguinte, que contém alguns passos intermédios para resolver a Torre de Hanoi com $4$ discos:


Primeiro mudamos os $3$ discos mais pequenos para a vara do meio em $T(3)$ movimentos...


Depois mudamos o disco maior para a vara livre em $1$ movimento...


Depois mudamos os $3$ discos mais pequenos da vara central para a vara mais à direita, em apenas $T(3)$ movimentos!

  - RGS

Popular posts from this blog

Tutorial on programming a memory card game

Image
Pt En Este post vai ser um tutorial, não muito detalhado, sobre como fazer um jogo de memória com Python e pygame. O jogo que vamos implementar é um jogo comum: viramos uma série de cartas para baixo e temos que as virar duas a duas, tentando encontrar os pares. Claro que quando viramos duas cartas que não são um par, temos de as voltar de novo para baixo. Quando estou a criar um jogo, gosto de o ir desenvolvendo por etapas funcionais: partir o processo em várias fases que representem pontos nos quais eu tenho algo que posso testar. Deste modo, não só o processo se torna muito mais interessante, como posso ir controlando o aspeto do que estou a produzir. Deixo de seguida uma lista das etapas que eu pensei para este projeto; cada ponto da lista descreve a funcionalidade que o jogo já suporta: Criar um ecrã onde mostro todas as cartas dispostas, face para baixo; Clicar em cima de uma carta faz com que ela se vire para cima; Clicar na segunda carta verifica se encontrei
Read more

Pocket maths: how to compute averages in your head

Pt En < change language Being able to do basic arithmetic calculations in your head is a great skill. Not because it is sexy but because it is useful in your daily life: it can help you check the change you are given when shopping, it can help you know if you will have enough money to pay for your groceries, it can help you estimate how much things cost after the discounts, etc... This often reduces to being able to sum and subtract decently; sometimes you need to make a couple of small multiplications, but that is it. More likely than not, you don't need to compute averages every day. But sometimes you just want the scoring average of your team for the past few games, or the average price per person of a given meal, or the average time you spent stuck in traffic this past week... And averages may appear nastier than simply adding or subtracting, because averages also require you to perform a division: in fact, you have to add all the numbers you want and then d
Read more

Markov Decision Processes 02: how the discount factor works

Image
Pt En < change language In this previous post I defined a Markov Decision Process and explained all of its components; now, we will be exploring what the discount factor $\gamma$ really is and how it influences the MDP. Let us start with the complete example of last post: In this MDP the states are Hungry and Thirsty (which we will represent with $H$ and $T$) and the actions are Eat and Drink (which we will represent with $E$ and $D$). The transition probabilities are specified by the numbers on top of the arrows. In the previous post we put forward that the best policy for this MDP was defined as $$\begin{cases} \pi(H) = E\\ \pi(T) = D\end{cases}$$ but I didn't really prove that. I will do that in a second, but first what are all the other possible policies? Well, recall that the policy $\pi$ is the "best strategy" to be followed, and $\pi$ is formally seen as a function from the states to the actions, i.e. $\pi: S \to A$. Because of that, we m
Read more