The naturals, the rationals and sets that fit inside themselves
If I have two groups of kids in front of me, for example two different classes, how can I decide if the two groups have the same size?
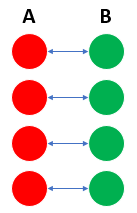
Of course I can count both groups, but I can also ask every kid from group $A$ to give his hand to a kid from group $B$, so they pair up. If, in the end, everyone is paired up, both groups have the same size.
If some kid from group $A$ doesn't manage to give his hand to anybody, because every kid from group $B$ is taken, then the group $A$ had more kids...
and if some kid from group $B$ doesn't get the hand from any kid from group $A$, then group $B$ had more kids!
When we want to compare the sizes of two sets this is one of the things we can do! Instead of counting the two sets, we can try to pair them up. If we manage to do that, the sets have the same size! Sometimes pairing two sets is a hard task and instead we opt for a different thing: remember that if $a \leq b$ and $b \leq a$ then $a=b$; hence, if a set $A$ is not smaller than a set $B$ and if that same set $B$ is also not smaller than the set $A$, then the two sets have the same size.
We will follow this train of thought to show that the set of natural numbers $\mathbb{N}$ and the set of rational numbers $\mathbb{Q}$ have the same size. To show that $\mathbb{Q}$ is not smaller than $\mathbb{N}$ , we can show that for any number $n \in \mathbb{N}$ there is a number $q \in \mathbb{Q}$ that is associated with $n$, and furthermore there are some numbers $q' \in \mathbb{Q}$ that are not associated with any natural $n$. If we write this association as a function $f: \mathbb{N} \to \mathbb{Q}$, we can take $f(n) = \frac{n}{73}$ for example. Function $f$ is injective, and that is what tells us that $|\mathbb{N}| \leq |\mathbb{Q}|$ (the notation |S| represents the cardinality of the set $S$, the size of $S$). In a way, we are seeing $\mathbb{N}$ as the group $A$ and $\mathbb{Q}$ as the group $B$ in the third image above.
We are left with showing that $|\mathbb{N}| \geq |\mathbb{Q}|$, which will let us conclude that $|\mathbb{N}| = |\mathbb{Q}|$. For that - if we keep seeing $\mathbb{N}$ as $A$ and $\mathbb{Q}$ as $B$ - we need to construct a situation similar to that of the second image. We will find a function $f: \mathbb{N} \to \mathbb{Q}$ that is surjective, i.e. for any number $q \in \mathbb{Q}$ there will be at least a natural that is associated with it. For some rationals $q$ it may happen that there are different naturals $n_1 \neq n_2$ such that $f(n_1) = f(n_2)$; that is, different naturals may be associated with the same rational. In the second picture, this may be seen as having every kid from group $A$ give his hand to a kid in group $B$, even if the kid from group $B$ is already taken:
Creating this function is easy and we present a sketch of how to calculate it:
The white squares are the naturals, and the position of the square determines $f(n)$. The line determines the numerator and the column the denominator, in such a way that $f(1) = 1$, $f(4) = \frac31$ and $f(13) = \frac{3}{2}$.
It is easy to see that the function represented by the table, which is filled diagonally - as the arrows suggest - is surjective and is also not injective: $f(1) = f(9) = 1$. Because it is surjective we have that $|\mathbb{N}| \geq |\mathbb{Q}|$. Because we already knew $|\mathbb{N}| \leq |\mathbb{Q}|$ we get $|\mathbb{N}| = |\mathbb{Q}|$, i.e. there are as many naturals as rationals, which is funny if we think that, on one hand, the naturals are inside the rationals and on the other hand there are plenty of rationals that are not naturals, that is $\mathbb{N} \subsetneq \mathbb{Q}$. When we are talking about finite sets, $A \subsetneq B$ means that $A$ is smaller than $B$, but that is no longer true if we are working with infinite sets... In a way, an infinite set is a set that fits inside itself...
We will follow this train of thought to show that the set of natural numbers $\mathbb{N}$ and the set of rational numbers $\mathbb{Q}$ have the same size. To show that $\mathbb{Q}$ is not smaller than $\mathbb{N}$ , we can show that for any number $n \in \mathbb{N}$ there is a number $q \in \mathbb{Q}$ that is associated with $n$, and furthermore there are some numbers $q' \in \mathbb{Q}$ that are not associated with any natural $n$. If we write this association as a function $f: \mathbb{N} \to \mathbb{Q}$, we can take $f(n) = \frac{n}{73}$ for example. Function $f$ is injective, and that is what tells us that $|\mathbb{N}| \leq |\mathbb{Q}|$ (the notation |S| represents the cardinality of the set $S$, the size of $S$). In a way, we are seeing $\mathbb{N}$ as the group $A$ and $\mathbb{Q}$ as the group $B$ in the third image above.
We are left with showing that $|\mathbb{N}| \geq |\mathbb{Q}|$, which will let us conclude that $|\mathbb{N}| = |\mathbb{Q}|$. For that - if we keep seeing $\mathbb{N}$ as $A$ and $\mathbb{Q}$ as $B$ - we need to construct a situation similar to that of the second image. We will find a function $f: \mathbb{N} \to \mathbb{Q}$ that is surjective, i.e. for any number $q \in \mathbb{Q}$ there will be at least a natural that is associated with it. For some rationals $q$ it may happen that there are different naturals $n_1 \neq n_2$ such that $f(n_1) = f(n_2)$; that is, different naturals may be associated with the same rational. In the second picture, this may be seen as having every kid from group $A$ give his hand to a kid in group $B$, even if the kid from group $B$ is already taken:
It is easy to see that the function represented by the table, which is filled diagonally - as the arrows suggest - is surjective and is also not injective: $f(1) = f(9) = 1$. Because it is surjective we have that $|\mathbb{N}| \geq |\mathbb{Q}|$. Because we already knew $|\mathbb{N}| \leq |\mathbb{Q}|$ we get $|\mathbb{N}| = |\mathbb{Q}|$, i.e. there are as many naturals as rationals, which is funny if we think that, on one hand, the naturals are inside the rationals and on the other hand there are plenty of rationals that are not naturals, that is $\mathbb{N} \subsetneq \mathbb{Q}$. When we are talking about finite sets, $A \subsetneq B$ means that $A$ is smaller than $B$, but that is no longer true if we are working with infinite sets... In a way, an infinite set is a set that fits inside itself...
Se eu tiver à minha frente dois grupos de miúdos, por exemplo de duas turmas diferentes, como é que eu posso decidir se esses grupos têm o mesmo tamanho? Claro que posso contar cada um dos grupos, mas também posso pedir que cada miúdo do grupo $A$ dê a mão a um miúdo do grupo $B$, para formarem pares. Se no fim toda a gente estiver emparelhada, os dois grupos tinham o mesmo tamanho.
Se algum dos miúdos do grupo $A$ não conseguir dar a mão a mais ninguém, por todos os miúdos do grupo $B$ estarem tomados, então o grupo $A$ tinha mais miúdos...
e se algum dos miúdos do grupo $B$ não receber a mão de nenhum miúdo do grupo $A$, é porque o grupo $B$ tinha mais miúdos!
Quando queremos comparar o tamanho de dois conjuntos, isto é uma das coisas que podemos fazer! Em vez de contar os dois conjuntos, podemos tentar emparelhá-los. Se conseguirmos, os dois conjuntos têm o mesmo tamanho! Por vezes emparelhar os dois conjuntos é complicado, então opta-se por uma via alternativa: se $a \geq b$ e $b \geq a$, então tem de ser verdade que $a = b$. Assim, se eu mostrar que o grupo $A$ não é mais pequeno que o grupo $B$ e se de seguida mostrar que o grupo $B$ não é mais pequeno que o grupo $A$, então os dois grupos têm o mesmo tamanho.
Vamos seguir esse raciocínio para mostrar que o conjunto dos números naturais $\mathbb{N}$ e o conjunto dos números racionais $\mathbb{Q}$ têm o mesmo tamanho. Para mostrarmos que o conjunto $\mathbb{Q}$ não é mais pequeno que $\mathbb{N}$, podemos mostrar que para cada número $n \in \mathbb{N}$ há um número $q \in \mathbb{Q}$ que lhe está associado, e para além disso alguns números $q' \in \mathbb{Q}$ não foram associados a nenhum $n$. Se escrevermos essa associação como uma função $f: \mathbb{N} \to \mathbb{Q}$, então podemos tomar, por exemplo, $f(n) = \frac{n}{73}$. A função $f$ é injetiva, e é isso que nos diz que $|\mathbb{N}| \leq |\mathbb{Q}|$ (a notação $|S|$ representa a cardinalidade do conjunto $S$, o tamanho de $S$). No fundo, estamos a ver $\mathbb{N}$ como o grupo $A$ e $\mathbb{Q}$ como o grupo $B$ na terceira imagem acima.
Falta-nos mostrar que $|\mathbb{N}| \geq |\mathbb{Q}|$, o que permitirá concluir que $|\mathbb{N}| = |\mathbb{Q}|$. Para isso - se continuarmos a ver $\mathbb{N}$ como $A$ e $\mathbb{Q}$ como $B$ - precisamos de construir uma situação semelhante à da segunda figura. Vamos arranjar uma função $f: \mathbb{N} \to \mathbb{Q}$ sobrejetiva, i.e. para cada número $q \in \mathbb{Q}$ vai haver pelo menos um natural que lhe corresponde. Para alguns racionais $q$, vai acontecer existirem naturais diferentes $n_1 \neq n_2$ tais que $f(n_1) = f(n_2)$; ou seja, naturais diferentes vão corresponder ao mesmo racional. Na situação da segunda figura, vamos fazer com que todos os miúdos do grupo $A$ que ainda não têm ninguém, passem a dar a mão a algum miúdo que já tenha par:
Criar esta função é fácil e ilustramo-la com um boneco:
Os quadrados brancos são os naturais e a posição do quadrado determina a que racional está associado: a linha determina o numerador e a coluna o denominador, de tal modo que $f(1) = 1$, $f(4) = \frac31$ e $f(13) = \frac{3}{2}$.
É fácil de ver que a função representada pela tabela, que é preenchida diagonalmente - de baixo para cima como as setas indicam - é sobrejetiva e também não é injetiva: $f(1) = f(9) = 1$. Por ser sobrejetiva temos que $|\mathbb{N}| \geq |\mathbb{Q}|$. Porque já sabíamos também que $|\mathbb{N}| \leq |\mathbb{Q}|$ decorre que $|\mathbb{N}| = |\mathbb{Q}|$, i.e. há tantos naturais quanto racionais, o que é engraçado se pensarmos que, por um lado os próprios naturais estão dentro dos racionais e por outro lado há racionais que não são naturais, ou seja $\mathbb{N} \subsetneq \mathbb{Q}$. Quando estamos a falar de conjuntos finitos, se $A \subsetneq B$ então $A$ é mais pequeno que $B$, mas isso deixa de ser verdade quando estamos a falar de conjuntos infinitos... De certa forma, um conjunto é infinito quando cabe dentro de si próprio...
Vamos seguir esse raciocínio para mostrar que o conjunto dos números naturais $\mathbb{N}$ e o conjunto dos números racionais $\mathbb{Q}$ têm o mesmo tamanho. Para mostrarmos que o conjunto $\mathbb{Q}$ não é mais pequeno que $\mathbb{N}$, podemos mostrar que para cada número $n \in \mathbb{N}$ há um número $q \in \mathbb{Q}$ que lhe está associado, e para além disso alguns números $q' \in \mathbb{Q}$ não foram associados a nenhum $n$. Se escrevermos essa associação como uma função $f: \mathbb{N} \to \mathbb{Q}$, então podemos tomar, por exemplo, $f(n) = \frac{n}{73}$. A função $f$ é injetiva, e é isso que nos diz que $|\mathbb{N}| \leq |\mathbb{Q}|$ (a notação $|S|$ representa a cardinalidade do conjunto $S$, o tamanho de $S$). No fundo, estamos a ver $\mathbb{N}$ como o grupo $A$ e $\mathbb{Q}$ como o grupo $B$ na terceira imagem acima.
Falta-nos mostrar que $|\mathbb{N}| \geq |\mathbb{Q}|$, o que permitirá concluir que $|\mathbb{N}| = |\mathbb{Q}|$. Para isso - se continuarmos a ver $\mathbb{N}$ como $A$ e $\mathbb{Q}$ como $B$ - precisamos de construir uma situação semelhante à da segunda figura. Vamos arranjar uma função $f: \mathbb{N} \to \mathbb{Q}$ sobrejetiva, i.e. para cada número $q \in \mathbb{Q}$ vai haver pelo menos um natural que lhe corresponde. Para alguns racionais $q$, vai acontecer existirem naturais diferentes $n_1 \neq n_2$ tais que $f(n_1) = f(n_2)$; ou seja, naturais diferentes vão corresponder ao mesmo racional. Na situação da segunda figura, vamos fazer com que todos os miúdos do grupo $A$ que ainda não têm ninguém, passem a dar a mão a algum miúdo que já tenha par:
É fácil de ver que a função representada pela tabela, que é preenchida diagonalmente - de baixo para cima como as setas indicam - é sobrejetiva e também não é injetiva: $f(1) = f(9) = 1$. Por ser sobrejetiva temos que $|\mathbb{N}| \geq |\mathbb{Q}|$. Porque já sabíamos também que $|\mathbb{N}| \leq |\mathbb{Q}|$ decorre que $|\mathbb{N}| = |\mathbb{Q}|$, i.e. há tantos naturais quanto racionais, o que é engraçado se pensarmos que, por um lado os próprios naturais estão dentro dos racionais e por outro lado há racionais que não são naturais, ou seja $\mathbb{N} \subsetneq \mathbb{Q}$. Quando estamos a falar de conjuntos finitos, se $A \subsetneq B$ então $A$ é mais pequeno que $B$, mas isso deixa de ser verdade quando estamos a falar de conjuntos infinitos... De certa forma, um conjunto é infinito quando cabe dentro de si próprio...
- RGS
